| ProFootballLogic | ||||||||||
| ARTICLES | TEAMS | STATS | RATINGS | STANDINGS | GAMES | SCHEDULE | PLAYERS | METHOD | SPORTS | |
Analyzing Loyola-Chicago
By Michael Gertz
Saturday, March 31, 2018
Loyola-Chicago's cinderella Final Four run in the 2018 NCAA Tournament has been unquestionably surprising. But exactly how surprising is an intriguing question that is rather difficult to answer with a high level of certainty.
Our Model
Prior to the first real round, our NCAA Tournament Odds gave Loyola-Chicago only a 0.2% chance of advancing to the Final Four, and their 7.8 (net points per game better than the D-I average) rating was pretty typical for an 11-seed. While the 500-1 odds immediately seem like they must have been wrong based on the fact that the event actually happened, it's important to keep in mind how many miniscule odds we assign each tournament.
Each tournament we predict odds that each of the 64 teams will advance to each of the 6 subsequent levels of the tournament. That's 384 individual odds, and this tournament alone we count 42 other predictions in the 0.1%-0.3% range, none of which occurred. The numbers are likely similar for the previous 6 years we've made projections, meaning there are likely around 300 other equivalent predictions we've made, of which we don't believe any have occurred. The previous most unlikely advancement according to our odds that we can find is 7-seed Connecticut's championship run in 2014, which we assigned a 0.5% chance of occurring.
While it's always difficult to analyze anything based on a single event occurring, we were given reason to question our odds when David Hess (@AudacityOfHoops on Twitter) of TeamRankings.com informed us that compared to other website projections, ours was well on the low end:
| Odds For Loyola-Chicago in the Final Four | |
|---|---|
| Kenpom.com | 1.9% |
| TeamRankings.com | 1.4% |
| FiveThirtyEight.com | 0.8% |
| ProFootballLogic.com | 0.2% |
Regardless of which projection was closest to reality, this is a fascinating case to investigate some differences between models and how the range can be so wide.
Opponents and Vegas
Vegas future odds appear to have ranged anywhere from 30-1 to 90-1 for Loyola-Chicago to make the Final Four. That's a far cry from our 500-1, but Vegas futures aren't as representative of true odds as inidividual game odds. Because you can't bet against the futures, oddsmakers will often raise future odds above a typical vigorish to optimize their earnings in cases where the public will bet a similar amount of money regardless of the line. This is especially true for popular or "hot" teams, and at longer odds, where oddsmakers will also simply want to reduce their risk.
To get a better picture of where Vegas stood on Loyola-Chicago, we can look at the individual game odds. Loyola was an underdog in all 4 games, and when plugging the point spreads into our model, we get an implied chance of 2.7% that they would win all 4 games based off the odds at the time each game was played.
Of course, that 2.7% figure shouldn't be compared to those above, because it is based on Loyola playing the exact teams they did, rather than on the probabilities that they would play teams based on the likelihoods of other teams advancing. For instance, if we plug Loyola's actual opponents back into our original model, their odds of making the Final Four jump from 0.2% up to 0.7%, meaning the other upsets in the region over tripled their odds of winning 4 straight tournament games.
Similarly, if we shift our model's rating for Loyola-Chicago such that the actual opponent scenario likelihood goes from 0.7% to Vegas' 2.7%, we arrive at a team rating of 11.0 rather than 7.8. Then plugging that rating back into the original model gives a 0.8% chance of making the Final Four with probabilistic opponents. This would imply that at the higher rating, the other upsets still would over triple Loyola's Final Four odds, and the 0.8% figure is then somewhat comparable to the original odds listed for the different websites. Keep in mind, these Vegas odds also include the presumption that Vegas was able to price in an increased opinion of Loyola with each win, but also an increased opinion of their opponents, as they had also won. We will address this further later on.
Taking a Closer Look At Loyola's Season
Our NCAA Basketball Model features a sophisticated optimatization of team ratings to fully account for the large disparities in strength of schedule in college basketball, but the fact that our model only uses game point differentials does mean that occasionally it could miss the point for teams with extreme injury issues. It could also lag behind a well designed model that accounts for in-game statistics, but that is mitigated by the relatively long length of the season.
To see if our model could be missing anything in regard to Loyola-Chicago, let's take a detailed look at their game results. Below is a graph of all their games against D-I opponents. The vertical axis is the point differential in the game minus the expected point differential based on our rating for Loyola-Chicago and the opponent, and the location of the game. For instance, in their first game against Wright State, we have Loyola as the better team by about 6.6 points, and they have a 3.4 point advantage for being at home. Therefore, we expect them to win by 10. Though they won the game, they won by only 4, so the game is marked as 6 points worse than the expected result.
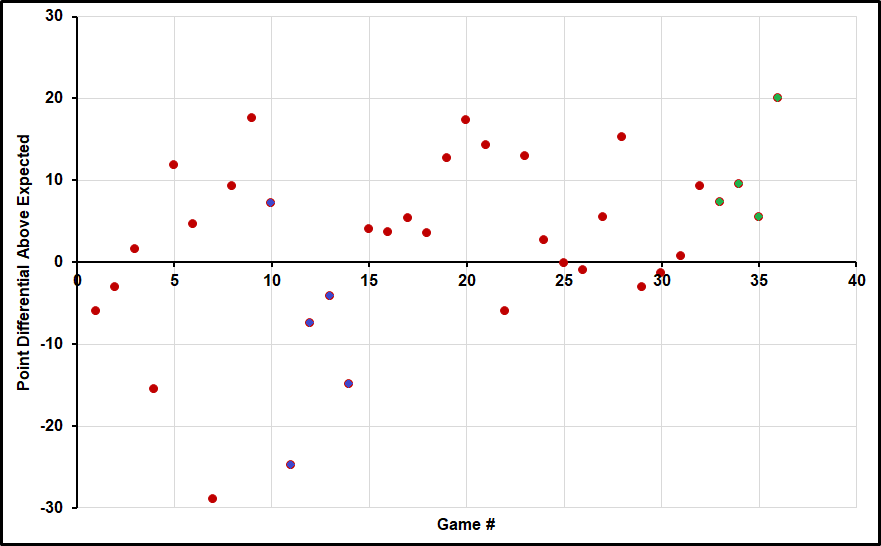
0 on the vertical axis represents a performance equal to our rating for Loyola-Chicago coming into the tournament (7.8 points better than the D-I average). And for instance, +10 would represent the average quality of a 17.8 rated team, around where we initially rated Michigan. While it looks like the average dot is well above 0, after ignoring the last 4 green dots from the actual tournament games, the average is actually just 1 point over Loyola's rating.
This difference is because our ratings use a sort of Bayesian prior based on the team's rating the previous seasons and things like recruiting ratings, as explained in the link above. It may appear that the prior failed in this case because it gave Loyola a rating lower than their results alone would imply, but overall the priors do make our ratings more accurate as a whole so we wouldn't dismiss it here.
Custer Injury
A potential pitfall for our Loyola-Chicago rating is a midseason injury that occurred to starting PG Clayton Custer. Custer led Loyola in scoring this season, and the Ramblers went 2-3 without him compared to only suffering 2 other losses all season. Further, they were 12 points/game worse in those 5 games than the other 27 games, after adjusting for opponents (as indicated by the blue dots for games 10-14 in the graph above).
That all sounds like it would massively throw off our Loyola rating, but the reality may not be so bad. Because it was only 5 games, even if we completely tossed them out, our Loyola rating would still only be about 2 points higher. On top of that, completely throwing them out would assume Custer is worth 10 points to Loyola, which is an astronomical number. It's reasonable to assume his impact is no more than half that, meaning at most our rating would only underrate Loyola by a point. It's also notable that Loyola-Chicago's best pre-tournament performance was in the game that Custer got injured and missed half of.
Other Trends
Even apart from the Custer injury, a quick look at the graph seems to show some obvious trends that we would warn against making too much of. It looks obvious that Loyola started the season slow, then perhaps started to "gel" midseason and play much better as their performances in the 2nd half of the season were much better, and even more consistent, than at the beginning of the season. And their NCAA Tournament performances in the last 4 dots seem to corroborate that.
In a way, Loyola's run doesn't look unusual at all, as the 4 tournament results are right in line with the rest of their 2nd half of the season. But it's important to keep in mind that those results were only good enough for wins in the first 3 games by 2, 1, and 1 points. Had they played in any of those games at the theoretical level they did in 3 of their final 4 pre-tournament games, they would have lost. Also, even at 50-50 odds each game, teams have only a 6.25% chance of winning 4 games in a row.
But as we rigorously tested in our article on whether teams get "hot", the case for teams undergoing such improvements over the season based on this data is extremely weak barring any further outside reasons for such improvement. In fact, teams show trends in performance like this at a level almost identical to what would be expected from randomness alone. That's not to say for certain that Loyola didn't improve, just that such a claim would need to be backed up by some more detailed information or game stats rather than point differentials alone.
Conditional Advancement
Our advancement odds use a single rating for each team for every round of the NCAA Tournament. As far as we can tell, FiveThirtyEight does the same (although they do update ratings once the tournament has actually begun in real life). One clever thing David Hess pointed out that TeamRankings.com does is use a range of ratings for each team in their simulations. Because no team ratings can be 100% confident, the most accurate method is to actually establish a probability distribution for the likehood that a team has various ratings.
This makes no difference in projecting a single game, but it does slightly adjust how tournament advancement odds play out. For instance, in estimating Loyola's odds to make the Final Four, it is important to keep in mind the fact that in that scenario they already made the Elite Eight. And in doing so have already shown that their rating coming in was more likely than not an underestimate.
Using varying team ratings is actually something we did when we used to make season and playoff simulations for the NFL based off automated ratings. We decided to calculate exact odds for the NCAA Tournament rather than doing simulations, which aren't as precise unless you do a huge number of them. But in the process we overlooked the error that can produce by underestimating very rare events.
Oddly enough, in this case the real life Loyola-Chicago may have actually experienced the opposite effect from what using a range of ratings would project. In general, we would expect that method to favor deep advancement by an underdog like Loyola since their wins at each stage would be relatively more surprising than those of good teams. But in this case the wins by Loyola's opponents were arguably more surprising.
In FiveThirtyEight's ratings, Loyola improved more than Tennessee due to their initial wins, but their rating actually increased much less than Nevada and Kansas State by the time they played those teams. Generically, you might expect that big underdogs would have the most to gain from the simulation process with a range of ratings. But in this case Loyola's easy path was even more influential in the opposite direction, so the other upsets that laid that path actually counteracted the theoretical benefit Loyola should have had. This is of course also partially due to fact that Loyola won their first 3 games by only a combined 4 points.
Exponentiality and Projecting Rare Events
Many linearly increasing things are erroneously said to be "increasing exponentially", but sports do provide a few actual cases of exponentiality that can throw off intuitions and projections alike. In this case, we are considering multiple rounds of advancement in a tournament. Therefore, in calculating the odds of such scenarios, individual game odds are multiplied together. Because of this, minor differences in team ratings essentially are compounded exponentially.
This is why different websites or models often can have vastly different advancement odds (like ours having Loyola 10 times less likely to make the Final Four than others) even if they have somewhat similar overall team ratings. This exponentiality makes projecting tournament results very difficult, and also explains why oddsmakers are particularly risk-averse when providing lines on such events.
In general, exponentiality increases variability greatly, and increases in variability have the largest relative impact on projections of very rare events. This is why rare events are the easiest to underestimate, and require the most caution in looking for potential exponentiality when assessing. It's possible that this reality increased the impact of our model not using conditional simulations when it came to Loyola-Chicago.
A good example of this was the Patriots 2nd half comeback from down 28-3 against the Falcons in Super Bowl 51. Many extremely low odds have been cited about what the Patriots win percentage may have been at it's lowest in that game, and they all were likely way off. That's because huge comebacks require exponential results in the form of many things all having to happen in one direction in a row.
Because most win percentage models are either based on generic past games or only partially adjust for which teams are playing, they are very useful in most cases but can easily fail at the extremes. Being a very good team, the Patriots likely had a bit better chance of scoring desperation touchdowns (and getting defensive stops) than the models expected, and those slight differences were multiplied because they needed scores and stops on several straight possessions. Further, the improvements in passing in the NFL in recent years means the models likely lagged in projecting comebacks because they were based on past years' data. That small difference also becomes amplified in the case of extreme comebacks.
Conclusions
Ultimately, we didn't write this article to try to defend our odds or say that any other website's odds are necessarily better overall, but to further invite readers into the ins and outs of our rating model and see a real life case of how different assumptions that go into a model can affect individual projections. Ultimately, it's fair to say that our Loyola rating could have been up to 1 point too low due to Custer's injury. But it could also be the case that the average NCAA Tournament team would require relatively similar upgrades (at least those that didn't have injuries during the tournament).
But beyond that, we don't really see any justification for Loyola having a higher rating based on their point differentials coming into the tournament. At least not based on assuming they got hot, or tossing out our preseason prior -- two assumptions in our model that have had a lot of predictive strength at large sample sizes.
It may be the case that deeper in game stats could reveal that they actually did improve over the season, or simply were better than their point differentials all along (for instance maybe they were particularly prone to taking it easy on opponents when they had a big lead). But keep in mind that such an analysis would also have to provide a reason as to why such improvements don't also show up in point differentials any more than randomness would expect.
That said, our initial Loyola-Chicago Final Four projection was probably also a bit lower than it should have been because we didn't take into account the conditional nature of the further rounds of the tournament by providing for a distribution rather than a single value as a team rating. Even if, as it turned out, that method may have projected a bigger benefit than what actually occurred.
Going Forward
Loyola-Chicago comes into the national semifinal as 5.5 point underdogs against Michigan, which is pretty much in line with where Vegas has ranked Loyola all along -- higher than us, but still not nearly as high as assuming they're hot and making a rating based on their last half of the season alone would imply. And while another win, or even close loss, would make us further question our initial rating, or a 15 point loss would feel like vindication, in reality just 1 more data point either way won't be too significant toward the analysis.
But short of clear evidence that Sister Jean is charming the officials, we still have yet to see a convincing case that Loyola's run isn't at least vaguely close to as miraculous as the 0.2% we initally projected.
| Recent Articles |
|---|
| If 2021 Had 16 Games - 1/10/22 |
| Wk 18 Playoff Scenarios 2021 - 1/8/22 |
| Wk 17 Playoff Scenarios 2020 - 1/1/21 |
| Wk 17 Playoff Scenarios 2019 - 12/27/19 |
| 2 Week Playoff Scenarios 2019 - 12/21/19 |
| 3 Week Playoff Tiebreakers 2019 - 12/11/19 |
| NFL Injury Point Value - 6/18/19 |
| How Teams Value Draft Picks - 4/25/19 |
| Analyzing The Zion Injury - 3/21/19 |
| Week 17 Playoff Scenarios 2018 - 12/27/18 |
| BUF | MIA | NE | NYJ | BAL | CIN | CLE | PIT | HOU | IND | JAC | TEN | DEN | KC | LV | LAC | |||||||||||||
| DAL | NYG | PHI | WAS | CHI | DET | GB | MIN | ATL | CAR | NO | TB | ARI | LAR | SF | SEA | |||||||||||||
| ProFootballLogic.com welcomes questions, requests, and error reports by email to contact@profootballlogic.com | ||||||||||||||||||||||||||||
| Privacy Policy | ||||||||||||||||||||||||||||
| Copyright © 2025 ProFootballLogic.com. All Rights Reserved. | ||||||||||||||||||||||||||||